Introduction to MATLAB Tutorial

In this article, we are giving an introduction to MATLAB. This article is part of a tutorial series we are developing for MATLAB. We hope you to give us feedback, so that we can improve our MATLAB tutorial series.

What does MATLAB stand for?

MATLAB stands for MATrix LABoratory. Hence, as the name suggests, here you play around with matrices.  Using MATLAB an image (or any other data like sound, etc.) can be converted to a matrix and then various operations can be performed on it to get the desired results and values. Image processing is quite a vast field to deal with. We can identify colors, intensity, edges, texture or pattern in an image. In this tutorial, we would be restricting ourselves to detecting colours (using RGB values) only.

Getting acquainted with MATLAB environment

For those who have just finished installing MATLAB on their system and can’t figure out from where to start, no need to worry! This tutorial will first make you well acquainted with its very basics and then move further.

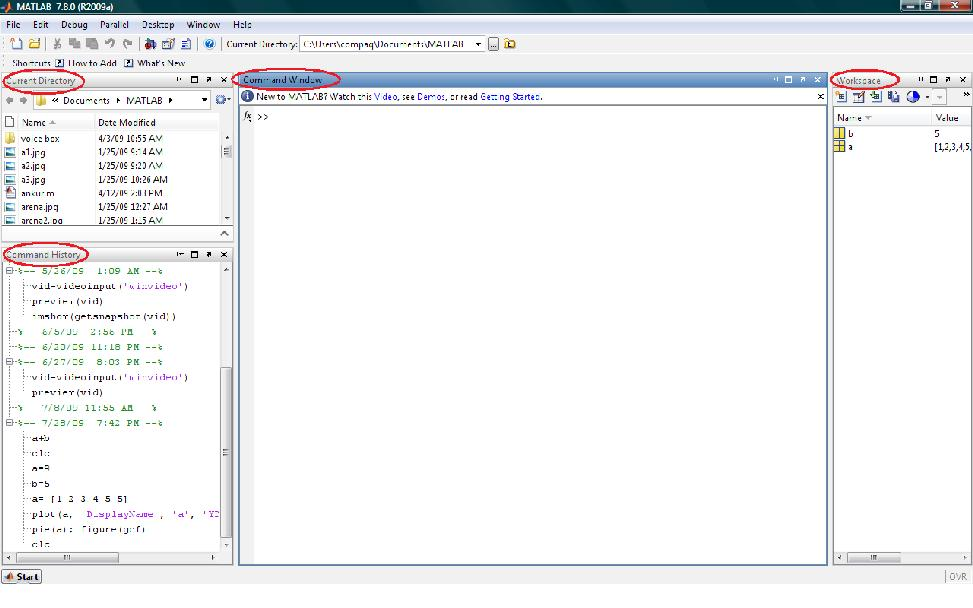
So, a typical MATLAB 2009 window looks like the image shown below.

MATLAB - 2009 - Home Screen

As marked in the image, there are 4 main windows.

Command window: This is the main window where you write the commands, as well as see the outputs. In other words, here is your interaction with the software.

Command History: As the name suggests, it shows the list of the commands recently used in chronological order. Hence, you can double click on a command to execute it again.

Current directory: It is the default directory (folder) for saving your files. All the files which you make (like m-files, as discussed later) are saved here and can be accessed from here directly. The location of the current directory is shown in the toolbar at the top. You can change it by changing the address here.

MATLAB - Change Directory Path

Workspace: It displays the list of the variables defined by you in the current session of MATLAB.

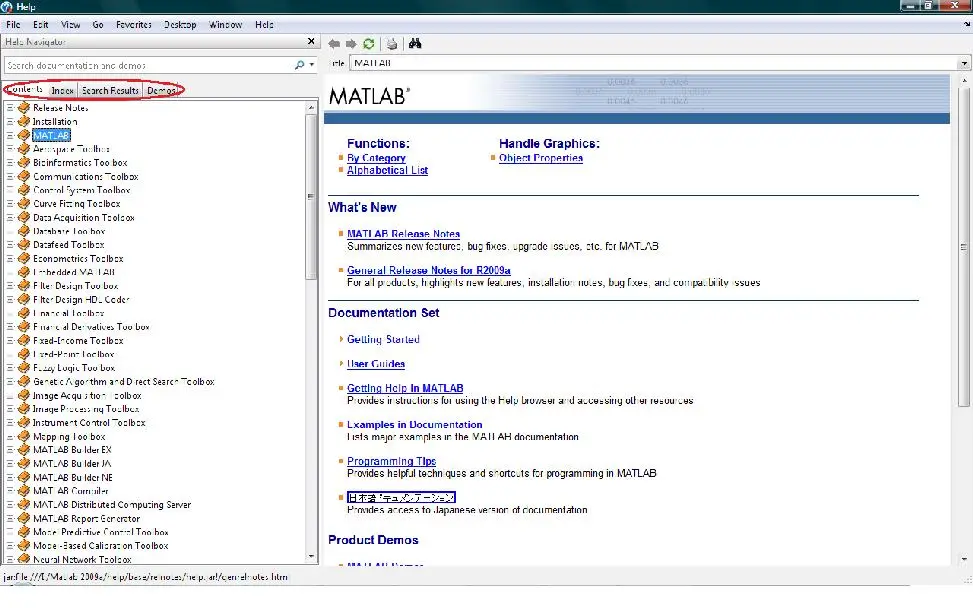
 The Menu bar and Toolbar: The  toolbar  has  buttons  for  common  operations  like  cut,  copy,  paste,  undo,  redo.  The  most important button here is the HELP button. It opens the MATLAB help window which  looks as the screenshot given below.

MATLAB - Help Page

 You can  get  the  details  of  any  MATLAB  command/function  here  and  many  demos  of  some commonly used applications. Locate the four tabs: Contents, Index, Search Results and Demos on the left. One of the best ways to learn by yourself is to look for demos of your interest and type the command/ function which you encounter there as the search term. You will then get the complete details of the function like its use, syntax, as well as few examples on how to use it. You can also have a look at some of the related functions at the end of page under the heading “See Also”. The demos related to Image Processing can be found under Image Processing Toolbox and Image Acquisition Toolbox.

Now once we are done with knowing the essential features of MATLAB, let’s start typing something in the command window, say: a=5 and press enter.

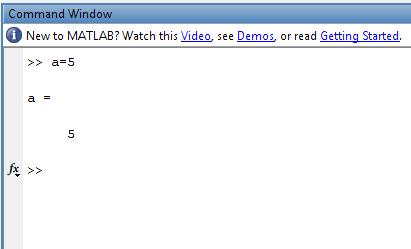
Yes… as you can see that MATLAB creates a variable with name ‘a’, stores value 5 in it and displays it in the command window itself. Hence you can see how user-friendly MATLAB is.
Variables are stored in the form of Matrices in MATLAB. Hence, ‘a’ is a 1X1 matrix in the above example. Similarly, you can make one dimensional, two dimensional, etc. matrices as follows:

>> a=[1 3 5 7 9]
a =
1     3     5     7     9
>> b=[1 2 3;4 5 6;7 8 9]
b =
1     2     3
4     5     6
7     8     9

To avoid the display of the variable, we use semi-colon (;) at the end of instruction.

 >> b=[1 2 3;4 5 6;7 8 9];

The indices of matrices in MATLAB start from 1 (unlike C/C++ and Java where they start from 0). We refer to a particular element of the matrix by giving its indices in parenthesis ().

>>  b(2,1)
ans =4

Now  with  the  variables  in  hand,  you  can  perform  various  mathematical  operations  on  them directly.

 >> a=[1 2 3];
>> b=[6 7 8];
>> a+b
ans =
7     9    11

ans is the default variable of MATLAB. You can also store the result in another variable as

 >> c=a+b c =
7     9    11

General functions & commands in MATLAB

clc: To clear the command window, giving you a ‘clear screen’.
clear: To remove all variables from the workspace. This frees up system memory.

Trigonometric functions

For angle in radians-

 >> sin(1)
ans =0.8415

For angle in degrees

>> sind(30)
ans =0.5000

Inverse trigonometric-

 >> asin(1)
ans =1.5708
>> asind(.5)
ans =30.0000

Similarly we have cos(), cosd(), acos(), tan() and other functions.

The Colon Operator

The colon is one of the most useful operators in MATLAB. It can create vectors, subscript arrays, and  specify  for  iterations.  In  a  very  crude  language,  we  can  say  that  the  colon  (:)  means “throughout the range”.

j:k                      is the same as [j,j+1,...,k]

j:i:k                    is the same as [j,j+i,j+2i, ...,k] A(:,j)                  is the jth column of A
A(:,j:k)               is A(:,j), A(:,j+1),…,A(:,k)

A(:)                    is all the elements of A, regarded as a single column.

Example: 

>> a= [1 2 3; 4 5 6; 7 8 9]
a =
1     2     3
4     5     6
7     8     9

>> a(:,2:3)
ans =
2     3
5     6
8     9

Relational Operators

Operator	Description
==	Equal to
~=	Not equal to
<	Less than
<=	Less than or equal to
>	More than
>=	More than or equal to

Frequently used Functions & Commands

Conditional Statements

if, else: Execute statements if condition is true, false respectively.
Syntax:

if condition1 statement
elseif condition 2 statement
else
statement end

 Example:

a=10;
>> if a<10 b=a/2;
else
b=a*2;
end
>> b
b =20

*Note:  As  a  block  is  contained  in braces  {}  in  C/C++/Java,  a block  is  terminated  by  the  ‘end’statement in MATLAB.

LOOP-ing Commands

for: To create a loop – that is to execute a block of code specified number of times.
Syntax:

for variable = initval:endval statement
… statement
end

Example 

>>c=[1 2 3 4 5]; b=0;
>>for i=1:5 b=b+c(i); end
>> b
b =15

while: Again to create loop, that executes till a specified condition is true.
Syntax:

while condition statements
end

 Example:

>> c=2009; i=1; while c>1 b(i)=mod(c,10); c=c/10; i=i+1; end
>> b
b =9.0000    0.9000    0.0900    2.0090

zeros(): Create array/matrix of all zeros.
B = zeros(n) returns an n-by-n matrix of zeros.
B = zeros(m,n) returns an m-by-n matrix of zeros. Example,

>> z=zeros(2,4)
z =

0	0	0	0
0	0	0	0

Similarly we have ones() function for all values 1.
size(): Returns matrix dimensions.
Example:
for the above matrix z,

>> size(z)
ans =
2     4

length(): Returns the length of a vector. For an array, it returns the size of the longest dimension.
Example:

>>x = ones(1,8);
>>n = length(x)
n =8

dot(): Returns dot product of two vectors.
Example:

C = dot(A,B)

sqrt(): Returns square root of each element of an array
min(): Returns smallest elements in an array.
Syntax:

C = min(A)

If A is a matrix, min(A) treats the columns of A as vectors, returning a row vector containing the minimum element from each column. Similarly we have max() function.
sort(): Sorts array elements in ascending or descending order
 Syntax:

B=sort(A,mode)

where value of mode can be

‘ascend’  :           Ascending order (default)
‘descend’ :           Descending order

plot(): Creates a 2-D line plot

So these all are the frequently used functions/commands in MATLAB. Until we come with our next chapter in MATLAB tutorial series, please share this article with your friends. Give us your feedback on improving the tutorial as well, we value it!